命題の解き方とコツ。真偽と対偶と逆と裏とは何かをわかりやすく。

学生時代には習い、社会人になるとSPIの問題で遭遇する”命題”。数学での命題とは、例えば、｢AならばBである｣のように、真偽(正しいか正しくないか)の判断対象となる文章を指します。解き方のコツとしては、対偶が一つのポイントとなるのですが、ここでは例題を挙げつつ、用語の意味を押さえて基本パターンを攻略できるようにわかりやすく説明していきます。

命題の用語

最初に押さえておきたいのは、用語の意味です。早速みていきましょう。

・真(しん)：命題が正しいとき → AならばBである

・偽(ぎ)：命題が間違っているとき → AなのにBがない

・対偶(たいぐう)：命題の対(つい)になるもの → BでないならばAでない

・逆(ぎゃく)：命題の反対 → BならばAである

なかなか言葉では難しいですよね。

シンプルに図にしてみます。

命題関係図

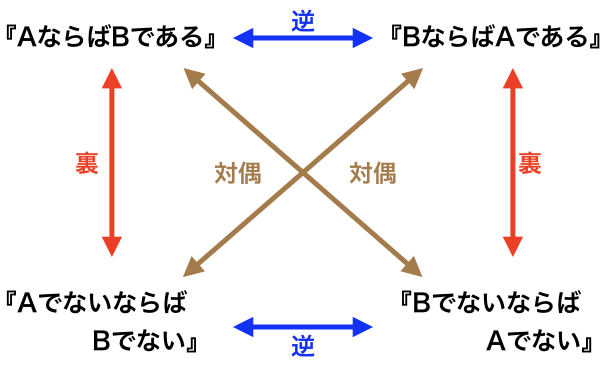
対偶と逆、裏を図にすると上記のようになります。用語の意味にとらわれ、難しく考えず、この図をイメージできることが大切です。

そして、問題の解き方でポイントとなるのが、対偶関係にある命題を考えることで、

『ある命題が”真”である場合、その対偶関係にある命題も”真”になる』

という関係性です。

例えば、”パソコンをする人は目が悪い”という命題が”真”の場合、”目が悪くなければパソコンをしないい人”という対偶も”真”になります。

問題の解き方のポイント

先述した、ある命題が”真”である場合、その対偶関係にある命題も”真”になるという考え方を基本として、実際に解く際には、これを“記号”で表すと時間が削減できます。

記号？？

記号といっても” ○ と X “で表せば良いのです。解き方を順番にみてみます。

例えば、”仕事ができる人は余裕がある人”とあった場合、

仕事ができる人→○　余裕がある→○
対偶を考えます。記号で表すならば、この場合両方”X”になれば良いので
X→余裕がない X→仕事ができない
命題が真であれば、その対偶も真なので
“余裕がない人は仕事ができない人”というのが真になります。

このように順番に考えていきましょう。

新たな命題

少し応用になる場合、２つの命題が成立するとき、正しいものは〜という問題が出てきます。この際も慌てず、基本に忠実に考えていくと見えてきます。

先ほどの例に付け加えてみます。

“仕事ができる人は余裕がある人”、”余裕がある人は効率的である”この２つが成立するとき、

仕事ができる人→○　余裕がある→○
対偶：X→余裕がない X→仕事ができない
余裕がある人→○　効率的→○
対偶：X→効率的でない　X→余裕がない
②と④を繋げてみる
“仕事ができない人は効率的でない”

繋げることで⑥の新しい命題ができるのです。

まとめ

基本パターンを紹介しましたが、”BでないならばAでない”という命題が核になる場合ももちろんあります。しかし、上記で説明してきた考え方を守れば解くことができます。

簡単計算関連 → 確率　順列/組み合わせ　通過算/流水算　 n進法　集合/ベン図

年齢算　仕事量　速度/距離/時間　旅人算　つるかめ算　食塩水の濃度数列

ポイントを整理しましょう。

ある命題が”真”である場合、その対偶関係にある命題も”真”である。
命題の文でのAとBを” ○とX “にしてみる

この２点をポイントに解いていくことが重要です。これは、2つの命題が出てきても変わりません。SPI問題を解かなくてはいけない機会のある方は、問題数を解いて慣れることも必要です。