組み合わせ計算は何通り。重複も合わせる順列との違いを簡単攻略。
投稿日:2018年6月27日 更新日:
これとこれの選び方は何通りの組み合わせになるのかな。今では、自動計算できるサイトも存在しますが、実際の詳細が気になる方もいるのではないでしょうか。これは、場合の数とも呼ばれる、”順列と組み合わせ”という計算で行われます。重複が考慮されているのはどちらだっけ。計算自体は決して難しいものではありません。これを機に両方の意味や違い、計算方法を学んで吸収しましょう。
組み合わせと順列の違い
まずは、”順列”と”組み合わせ”の違いは何なのかをみていきましょう。
例えば、A,B,C,Dという4つの文字があったとします。この中から2つの文字の並べ方(選び方)は何通り?とあったとします。
これは、『4 x 3=12通り』となります。※計算は、後述しますので、ここでは考えなくてOKです。
この12通りを列挙してみます。
「AB,AC,AD,BA,BC,BD,CA,CB,CD,DA,DB,DC」の12通りです。
最初にAを選ぶと次に選ばれるのは、B,C,Dのどれか3つです。最初にBを選びと次に選ばれるのは、A,C,Dのどれかになります。つまり、最初は4つから選べますが、2番目に選べるのは3つになるということです。これを続けると上記のようになりますよね。
これを『順列』といいます。※意味は、整理して後述します。
そして、この12通りの中で、ABとBAは、並び方は違いますが、4つの文字から2つの文字を選ぶ選び方は同じと考えてみます。
「AB,AC,AD,BA,BC,BD,CA,CB,CD,DA,DB,DC」の12通りのうち、
・AB=BA
・AC=CA
・AD=DA
・BC=CB
・BD=DB
・CD=DC
この6通りは、同じ選び方、一緒のもの、つまりは“重複したもの”とします。すると、先ほどは、12通りありましたが、重複が6通りあるので、12通り−6通り=6通りとなります。
これを『組み合わせ』といいます。
順列は、違う選び方、別のもの、つまりは重複したものではないと考えています。
つまり、
あるn個のものからr個選んで、
・「順序よく1列に並べて。並び方が逆でも重複したもの(無視)としないで並べてね。」
これが『順列』です。
・「順序は気にしないけど、並びが逆だったら重複したもの(無視しないで)として選んでね。」
これが『組み合わせ』です。
つまり、あるn個のものからr個、並べるまたは選ぶ場合、
“並べ方”に拘る”順列”、”選び方”に拘る”組み合わせ”と考えると
区別がつき易くなるのではないでしょうか。
この例を用いて、それぞれの計算式の公式を説明していきます。
順列の公式
“あるn個のものからr個を順番に1列に並べる”場合の数。
*並べ方がABでもBAでも気にせず並べる(重複してるとはしない)*
この場合の数の値を”P”を用いて、計算式を表します。
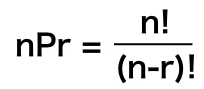
となります。
この” ! “は、階乗と呼ばれ、
n! = n x (n − 1) x (n − 2) x (n − 3) … x 1
の計算式で示します。最後“カッコ内”が ” x 1″ になるまで”かけ算”をしていきます。
最初の並べ方が、n通り
2番目の並べ方が、(n − 1)通り
3番目の並べ方が、(n − 2)通り
となることを意味しています。
先の例、A,B,C,Dの文字4つから2つの並べ方を計算式に入れると、
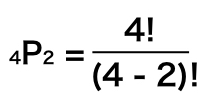
となります。
そして、分子の ” n! ” に当たる ” 4! ” から計算してみます。
4! = 4 x 3 x 2 x 1
分母の ” (4 – 2)! ” は、” 2! ” となるので
(4 − 2)! = 2 x 1
これらを分母分子に戻します。
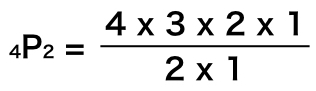
分母分子の ” 2 x 1 “は約分できるので、
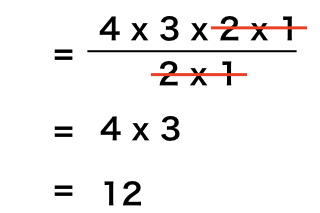
答えは、12通りとなり、列挙して計算している最初の段落に記述の答えと一緒になりました。
これらが”順列”の計算であり、公式となります。
組み合わせの公式
“あるn個のものからr個を順番関係なく選ぶ選び方”場合の数。
*並べ方がABとBAは同じとして気にして並べる(重複してるとする)*
この場合の数の値を”C”を用いて、計算式を表します。
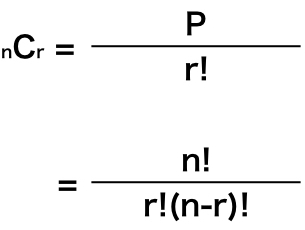
となります。
ここでの ” P “は、先ほどの順列の公式を表していますので、
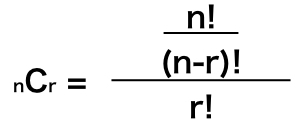
これを計算すると、上記2番目の公式に整理されます。
この” ! “は、先ほど同様、階乗となり、
r! = r x (r − 1) x (r − 2) x (r − 3) … x 1
の計算式で示します。最後 “カッコ内”が ” x 1″ になるまで”かけ算”をしていきます。
先の例、A,B,C,Dの文字4つから2つの選び方を計算式に入れると、
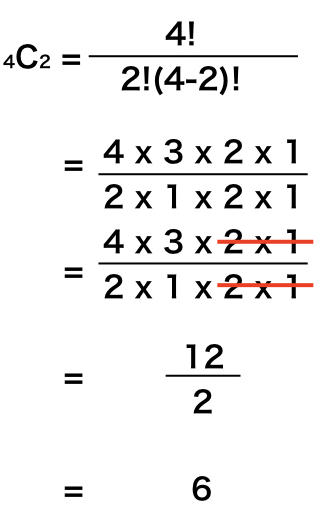
答えは、6通りとなり、重複した部分を考慮した列挙して計算している最初の段落に記述の
答えと一緒になりました。
これらが”組み合わせ”の計算であり、公式となります。
基本的には、上記公式を覚えておけば問題はないですが、約分できる部分が必ず出てくるので、
少し詳細を考えてみると、
![]()
つまり、あるn個のものから(n-r)個選ぶ組み合わせを計算することで同様の答えが得られます。
割愛しますが、先例を当てはめて考えてみてください。
” C “にはこのような性質があることを余裕があれば覚えておくと、計算が楽になります。
簡単計算関連:確率 速度/距離/時間 旅人算 通過算/流水算 仕事量 n進法
まとめ
例外にはなりますが、「サイコロ2つが偶数になるのは何通り。」や「サイコロ2つが○の倍数になるのは」を考える際は、1つ1つ列挙する方が早かったりもします。
さらに「少なくとも〜」という場合は、組み合わせの総数から1つもそうでない場合の総数を差し引くことで計算できることが多々あります。
さて、この順列と組み合わせの意味
あるn個のものからr個選んで、
・「順序よく1列に並べて。並び方が逆でも重複したものとしないで並べてね。」
これが『順列』です。
・「順序は気にしないけど、並びが逆だったら重複したものとして選んでね。」
これが『組み合わせ』です。
これをきちんとまずは押さえて、計算に慣れていきましょう。
スポンサーリンク
