食塩水の濃度計算。問題の簡単な解き方にする天秤算と求め方の公式
投稿日:2018年7月6日 更新日:
食塩水の濃度の解き方に出てくる濃度とは、食塩○gを水△gに溶かした、食塩水全体の重さ(食塩+水)に対しての食塩の重さの割合(%:パーセント)で表したものです。問題の解き方では、濃度の公式を用いるパターン、連立方程式そして、天秤算と言われるものがあります。天秤算は時短として用いられることが多いのですが、まずはそれぞれの基本を押さえて、簡単な解き方を得てください。
濃度の公式
 ※パーセント(%)は、全体を100としたときの割合
※パーセント(%)は、全体を100としたときの割合
例えば、食塩60gに水540gを溶かすと何%の濃度になるのか。という問題があった場合、
濃度 = 食塩60g / 600g(食塩+水) x 100 = 10%
となります。食塩水が、“食塩 + 水”の和(足し算)になることを忘れないようにしましょう。
連立方程式
続いて、一般的である連立方程式での解き方をみていきます。
例題:6%の食塩水と18%の食塩水を混ぜて、12%の食塩水600gを作ります。18%の食塩水は
何g必要か。
6%の食塩水を x 、18%の食塩水を y とします。
混ぜたら600gになるので、
x + y = 600・・・①
さて、もう一つの方程式は何でしょうか?ここでは、食塩の量もわかってません・・・
濃度の公式を確認してみましょう。濃度は、食塩を食塩水で割って、100をかけます。
“食塩 =”に変換すると、

となります。つまり、もう一つは食塩にスポットを当てて考えます。
6%の食塩水に含まれる食塩と18%の食塩水に含まれる食塩を混ぜるので、必然的に足せば12%の食塩水に含まれる食塩と同じになりますよね。つまり、
2つの食塩水の食塩の量は、混ぜてできた食塩水の食塩の量と一緒になる
実際当てはめてみましょう。食塩ベースで計算式を考えます。
0.06x + 0.18y = 600 x 12/100
0.06x + 0.18y = 72・・・②
この①と②が連立方程式の式になります。
②を計算しやすくしましょう。両辺100倍します。
6x + 18y = 7,200
x + y = 600より、
y = 600 − x・・・③
③を②に代入します。
6x + 18(600 − x) = 7,200
6x + 10,800 − 18x = 7,200
−12x = −3,600
x = 300
6%の食塩水は300gということです。つまり18%の食塩水も300gとこの問題ではなりました。
天秤算
簡単な解き方として紹介されるのが、この天秤算です。まずは、記号の位置関係を覚えてください。
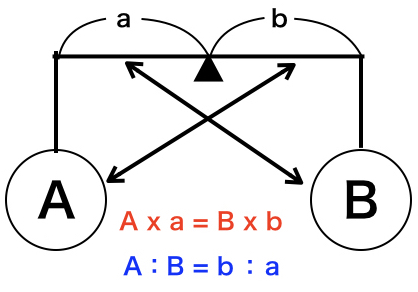
これをこの食塩水の問題に当てはめると次のような関係になります。
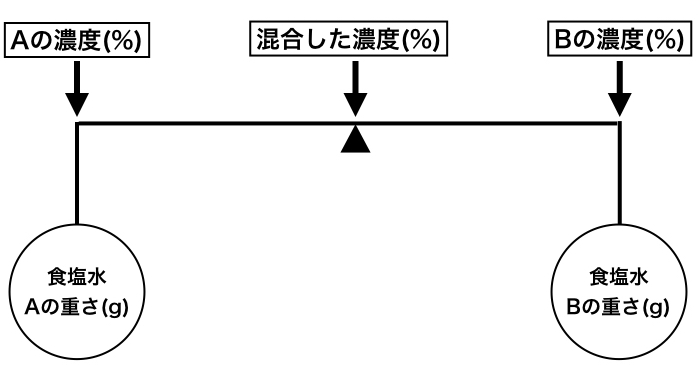
これで、先ほどと同じ例題を解いてみましょう。
例題:6%の食塩水と18%の食塩水を混ぜて、12%の食塩水600gを作ります。18%の食塩水は
何g必要か。
この問題を上記図に当てはめてみます。
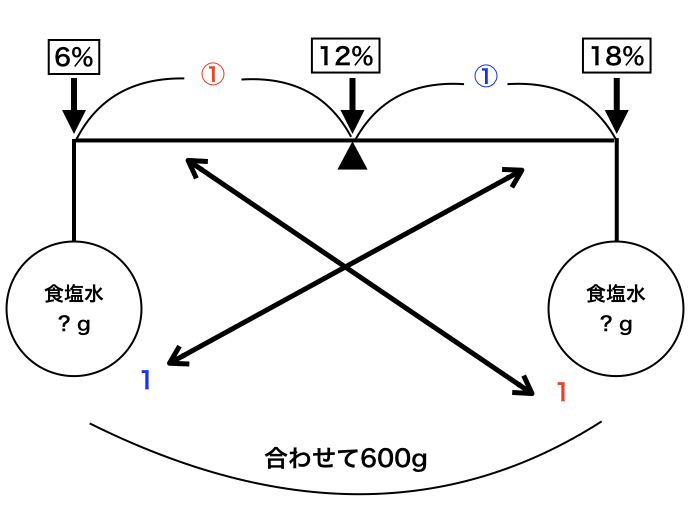
食塩水の重さは2つともわかりませんが、合わせて600gです。
濃度がわかっています。濃度の ” a:b “は ” 1:1 “。” A:B ” も ” 1:1 “。
a:b = 1:1
A : B = 1:1
食塩水は合わせて600gなので、各食塩水は半分(1/2)づつとなります。
600 ÷ 2 = 300
つまり、6%も18%も300gとなります。
この天秤算を使う際は、最初の図の関係を覚えて、下記の2点がポイントです。
・わかっていないのはどこか。(何を求めるのか)
・『A:B』 と『a:b』の関係(濃度と食塩水の重さで逆になる)
もう1問、例題を解いてみましょう。
例題:3%の食塩水200gと18%の食塩水300gを混ぜると、何%の食塩水になりますか。
これを図に埋めてみると、
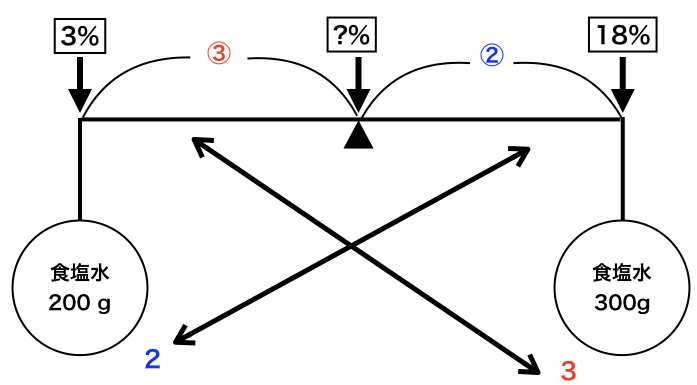
求めるのは、真ん中の濃度です。食塩水がそれぞれ200g、300gですので、
” A:B ” が ” 2 : 3 “になります。
『A:B = b:a』なので、” a:b ” は、” 3:2 “になります。
濃度も3%と18%とわかっているので、左側③部分を計算してみます。
(18 − 3 ) x 3/5 = 9%
右側②部分は、
(18 − 3 ) x 2/5 = 6%
③は、9%。②は、6%です。
両端は3%と18%なので、
3% + 9% = 12%
18% − 6% =12%
つまり、答えは、12%です。便宜上、両方を計算しましたが、片方で構いません。
簡単計算関連 → 確率 順列/組み合わせ 通過算/流水算 n進法
まとめ
どちらが早いか、やりやすさは、人によります。特に天秤算は、図をきちんとイメージできないとその後の計算に影響が出てしまいます。
連立方程式の”食塩”をベースとするもう一つの方程式、天秤算での比率が逆になること。これをポイントとして、忘れないようにしましょう。
さらに、計算している最中に、何を求めているんだっけ?とならないよう一つ一つ解いていくことが何より大切です。
スポンサーリンク
