数学の集合の解き方をわかりやすくするベン図の基本パターン計算。
投稿日:2018年7月11日 更新日:
“集合”という数学出ててくる問題は、学生の次は、就職試験のSPIで目にするのではないでしょうか。その時点では、すでに忘れてしまっていたりと。どちらかをみたすもの、どちらもみたすもの、どちらもみたさないなど、”みたす””みたさない”をの問題が”集合”と呼ばれるもので、この解き方として”ベン図(英語:venn diagram)”という視覚的にわかりやすい手法をとると、解き方としては簡単にできます。いわゆる数字の計算自体は簡単ですが、その計算をどのように考えていくのか、このベン図の基本図とそれぞれが何を意味しているかを確認しましょう。ここでは、基本となる問題から”円”が3つになったときなど、応用に触れていきます。
ベン図
早速ですが、これがベン図です。
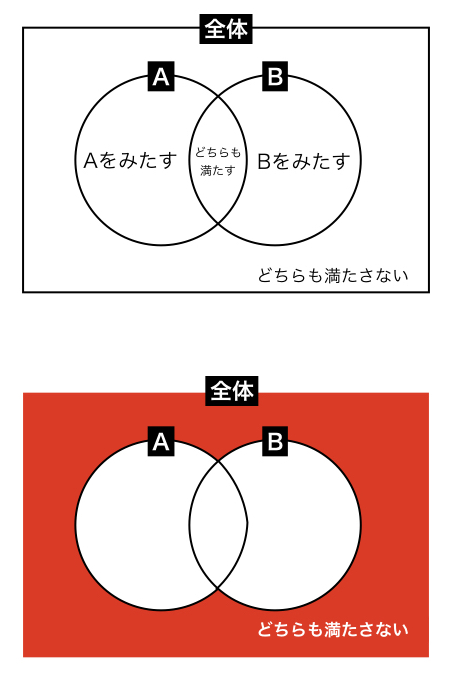
外の四角が全体の人数などを示しています。そしてAとBの円があり、円が重なっている部分もあります。
< AとBの各円 >
“Aをみたすもの”、”Bをみたすもの”がそれぞれ、その円の中に入ります。
< AとBの重なる部分 >
“AもBもみたすもの”、”どちらもみたすもの”が入ります。
< 円の外から全体の四角の中(下図の赤部分) >
“AもBもみたさない”、”どちらもみたさないもの”を意味します。
実際例題を見ていきましょう。
基本問題パターン1
例題:100人にアンケートをとると、通勤に電車を利用する人が82人、バスを利用する人が35人でした。また、どちらも利用しない人が5人いました。電車もバスも利用する人は何人ですか?
これをベン図にして見ましょう。すると、
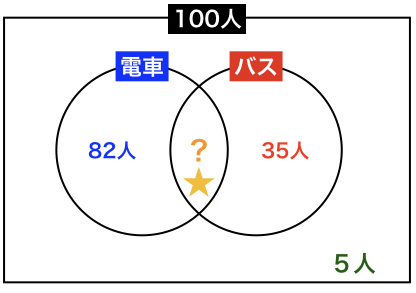
整理すると、
全部で100人(外の四角)、電車82人(青)、バス35人(赤)、どちらも利用しない5人(円の外から四角の間)。問われているのは、電車、バスのどちらも利用する人(星、?)部分です。さて、計算です。
まず、電車、バス、それぞれを利用する人を足します。
電車82人 + バス35人 = 117人
しかし、アンケートをとった人数は100人です。多いですよね。これは何を意味しているかというと、
電車、バス両方とも利用している人(円の重なっている部分)が電車、バス両方に含まれてしまっている。
つまり、「電車とバスの円、個々単体をみると82人、35人ですよ。」ということなのです。問題文などでは「どちらか一方をみたす」とも言います。
先ほどの117人、総人数100人、どちらも利用しない人の5人(緑)。これで計算します。
電車かバス、電車とバス両方を利用すると回答した人数の総数は、
100人(アンケート総人数) − 5人(どちらも利用しない人) = 95人
117人と95人、この差が「電車、バス両方利用しますよ。」と回答した人数になります。
問題文などでは「どちらもみたす」とも言います。
117人 − 95人 = 22人
これが答えになります。
ベン図を描いて、問われているのはどの部分かを考えることが大切です。
基本問題パターン2
例題:男女合わせて社員総数40人のある会社でメガネをかけている社員は25人です。男性社員は、20人います。このとき、メガネをかけている女性社員は何人以上何人以下ですか。
ここで考えなくてはいけないのは、2点です。
・女性社員は、最少で何人なのか。
・女性社員は、最大で何人なのか。
これを分けて考えることです。これをベン図で考えていきます。
< 女子社員が最少 >
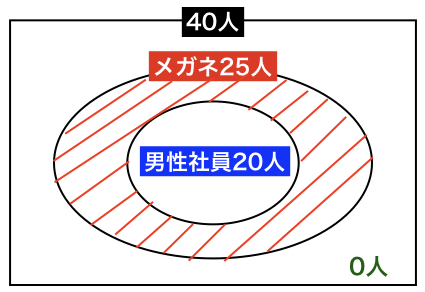
社員40人のうち、メガネをかけている社員が全員男性であった場合が、女子社員の最少となります。それを表すとメガネの円に男性社員の円が中に丸々入ることになります。
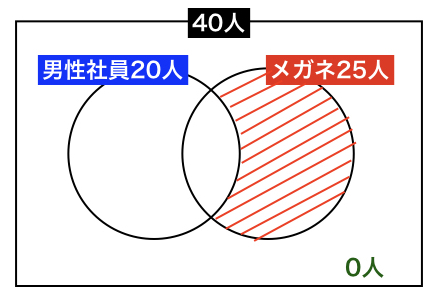
次に、最大を考えます。メガネをかけている社員が全員女性のときになります。違う言い方をすると、メガネをかけていない女性社員が0人(緑/円の外側から四角までの間)のときとなります。
それぞれ計算してみます。
最少:メガネをかけている社員が全員男性のとき
25人(メガネをかけている) − 20人(男性社員) = 5人
最大:メガネをかけていない女性社員が0人のとき = メガネをかけている社員が全員女性のとき
40人(総社員数) − 20人(男性社員) = 20人
つまり、メガネをかけている女性社員は5人以上20人以下となります。
応用パターン(3つの円)
基本的な見方は変わりません。円が1つ増えるだけです。
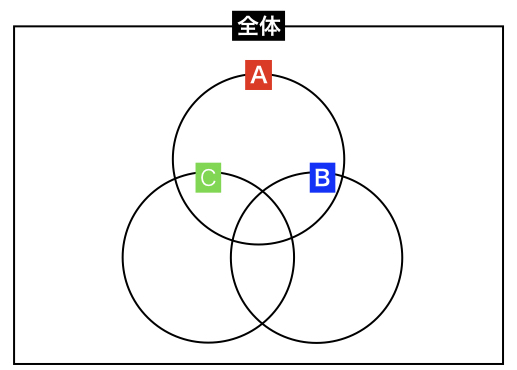
基本ベン図ですが、これが上記のようにA,B,Cの円全てが重なっていたり、重なっていなかったりします。それは、問題によりけりになるので、柔軟に対応する必要があります。
例題:50人にスポーツのアンケートを実施したところ、
・野球が好き 18人
・サッカーが好き 15人
・その他のスポーツ 10人
・野球もサッカーも好き 10人
・野球もその他のスポーツも好き 5人
・サッカーもその他のスポーツも好き 0人
この場合、どのスポーツも好きでない人は何人ですか。
これをベン図にすると、
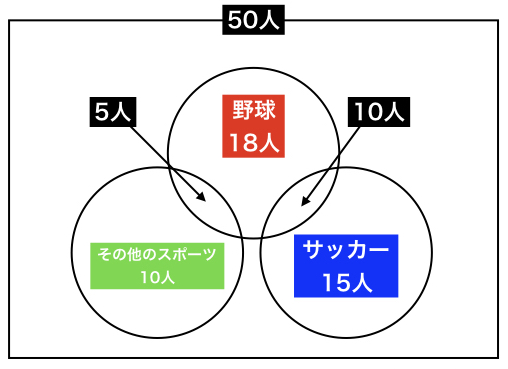
まず、選択肢のどれかのスポーツが好きな人(どれか一つをみたす人たち)は、
(野球 + サッカー + その他のスポーツ) − (選択肢の複数好きで重複する人たち)
(18 + 15 + 10) − ( 5 + 10 ) = 28人
アンケート総人数は、50人なので、求める”どのスポーツも好きではない人たち”は、
50人 − 28人 = 21人
となります。答えは、21人です。
これがもし、”サッカーもその他のスポーツも好き””3つとも好き”の人がいる場合は、3つの円の基本パターンのベン図となります。
簡単計算関連 → 確率 順列/組み合わせ 通過算/流水算 n進法
年齢算 仕事量 速度/距離/時間 旅人算 つるかめ算 食塩水の濃度
まとめ
解き方としては、ベン図の基本を抑え、
“基本問題パターン2″で”赤斜線”で示しましたが、問題文を見ながら、
・Aをみたすもの
・Bをみたすもの
・両方をみたすもの
・どれもみたさないもの
この4点のポイントを押さえましょう。そして、埋めていき、
“何を求めなくてはいけないのか”
これにブレがないようにすることが大切です。
スポンサーリンク
