数列の解き方。公式のような等差数列と等比数列の基本パターン。
投稿日:2018年7月14日 更新日:
数が並んでいて、それが”ある規則に則って並んでいるもの”。これを”数列”といいます。数列の種類は様々ありますが、SPIでの頻出は、同じ数を足していく(和)、引いていく(差)、『等差数列』または、同じ数をかける(積)、割っていく(商)、『等比数列』であることが多いです。ここでは、忘れてしまったの方に向け、この2つの基本を問題とともに説明していきます。公式を用いることで解くことができますが、数が少ない場合は、下手に計算するより、一つ一つ書き出す方が早く、簡単なときもあります。まずは、解き方を覚えてしまいましょう。
数列の考え方と用語
解き方を覚えるために、考え方と基本となる用語を押さえる必要があります。
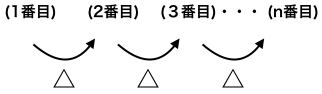
上記は、1番目からn番目まで△という規則で並んでいます。つまりは、1番目の数に△を足すのか、引くのか、かけるのか、はたまた割るのかで、2番目の数になることを表しています。
1番目から3番目までを考えると、3番目の数まで△は2個。これに倣うと4番目の数までは△が3個とイメージできるのではないでしょうか。
これにより、
『 (n番目)の数までの”△”は、(n − 1)個 』
と考えることができます。
これを基本として公式をみていきます。
公式
< 数列の公式 >

< 用語 >
・等差数列:同じ数を足すか(+)、引くか(−)
・等比数列:同じ数をかけるか(x)、割るか(÷)
等差数列の△を『公差(こうさ)』といい、等比数列の△を『公比(こうひ)』といいます。
また、n番目の数を『第n項』といい、最初(1番目)の数を『初項(しょこう)』といいます。
問題(等差数列)
例題1:5、7、9・・・と数字が並んでいるとき、40番目の数は。
“2”ずつ増えていく等差数列です。初項が5、公差が2です。そして40番目の数を求めるので、公式にそのまま当てはめると、
5 + (40−1) x 2 = 88
答えは88です。
例題2:初項が1、公差が5である等差数列において30番目の項は。
問題文での初項、公差の意味を理解していないと解けないですよね。
1、5、10・・・・と並んでいるとき、30番目の数はと聞かれているのと一緒です。これも公式そのまま当てはめます。
1 + (30−1) x 5
=146
上記の問題で、たとえ公差が“−△(マイナスの数)”であっても考え方は一緒なので、慌てないでください。
そして、上記の例で言えば、146は、何番目の項になりますか。という問題もあります。この場合、公式でのn番目がわかっていないので、それを”y”などにして公式に当てはめれば、解けます。
1 + ( y − 1 ) x 5 = 146
とすれば良いのです。するとy=30となって、30番目であると答えが出ます。
問題(等比数列)
例題1:5、10、20・・・と数字が並んでいるとき、7番目の数は。
” x 2 “ずつ増えていく等比数列です。初項が5、公比が2です。そして40番目の数を求めるので、公式にそのまま当てはめると、
5 x 2(7−1) = 320
答えは320です。公式に当てはめなくても順序よくかけ算をした方が早い方もいるでしょう。
例題2:初項が1、公比が5である等差数列において6番目の項は。
問題文での初項、公比の意味を理解していないと解けないですよね。
1、5、25・・・・と並んでいるとき、6番目の数はと聞かれているのと一緒です。これも公式そのまま当てはめます。
1 x 5 (6−1) = 3125
=3125
これらの問題も、たとえ公比が“−△(マイナスの数)”であっても考え方は一緒なので、慌てないでください。
簡単計算関連 → 確率 順列/組み合わせ 通過算/流水算 n進法 集合/ベン図
年齢算 仕事量 速度/距離/時間 旅人算 つるかめ算 食塩水の濃度
まとめ
ここでは、基本パターンの問題を例題として挙げました。まずは、
・数列とは何なのか。
・公式と解き方は。
これに慣れましょう。
そして、応用として、分数や最大の和となるのはというのも出てきますが、これも考え方の基本は一緒です。最大の和は、となる場合は、 ” ≧ (不等号)”を用いる必要があります。これは、実際問題を行わなくてはいけない状況で掴んでいくと良いです。
スポンサーリンク
