年齢算の方程式以外の解き方で簡単に解くやり方を身につける。
投稿日:2018年7月5日 更新日:
年齢算とは、親の年齢が子の○倍になるのは何年後。何年前。現在の年齢は。とこれらの計算を行うものです。子供が3人や4人になったり、両親の和との比較になったりする応用問題もあります。一般的に連立方程式にするのが、答えを導く解き方です。もちろんそれでも構いません。ここでは、連立方程式の方法とSPIで推奨される、より時間短縮になるやり方を説明してきます。両方を使えるようになって、どちらでも解けるようにしておけば、自身が問題によって使い分けることも可能なので、ぜひ覚えてみましょう。
年齢算の連立方程式の解き方
簡単な問題で進めていきます。
< 現在、父は30歳、子は4歳です。何年後に父の年齢が子の3倍になりますか。>
この場合は、連立方程式でなくても解けます。何年後をxとします。すると、
x年後の父と子の年齢は、(30+x)歳と(4+x)歳となります。この年齢で父の年齢が子の3倍になれば良いので、
30 + x = 3 (4 + x) が成り立ちます。計算していきましょう。
30 + x = 12 + 3x
30 − 12 = 3x − x
2x = 18
x = 9
つまり、9年後が答えになります。
ごく基本の問題が上記です。連立方程式にしなくてもこの問題の種類、例えば、両親がいて、その和が4人の子供の○倍になるときは何年後、何年前ですか。のような問いに使用できます。
続いて、このようなときには連立方程式になります。
< 現在、父と子の年齢の和は52歳。8年後に父の年齢は子の年齢の3倍になります。現在、父は何歳ですか。>
現在の父の年齢をx、子の年齢をyとします。年齢の和が52歳なので、
x + y = 52・・・①
8年後に父の年齢が子の3倍になるので、8年後の父と子の年齢は、
(x + 8) = 3 (y+8)・・・②
この①と②が成り立ちます。簡単にxかyを出してみます。ここでは①を使います。
①より、x = 52 − y
このxを②に当てはめましょう。
(52 − y) + 8 = 3 (y + 8)
60 − y = 3y + 24
4y = 36
y = 9
現在、子の年齢が9歳なので、父の年齢は、①から43歳となります。
連立方程式自体の解き方を含め、何をxにしたか、何をyにしたかを間違えずに考えれば、計算自体は難しくないです。
さて、やはり、方程式は・・・と苦手意識がある方は、次の方法を試してください。
年齢算の簡単な解き方
年齢算は、方程式で解くことができるのですが、もう一つ“線分図”を使用する方法もあります。
まず、線分図がどんなものかを説明します。
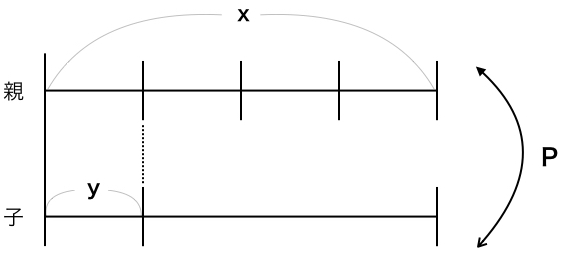
子の年齢が ” y ”
親の年齢が ” x ”
” P ” は、親と子の年齢の和(足し算)を示しています。
ここでのポイントは、親の各間隔は”等間隔”の図あることです。
上記の図では、親は子の年齢の4倍であることを示しています。
この線分図を使う際、
・各間隔は等間隔であることを示している。
・親と子の年齢差は” x−y”部分になる。
・Pは、親子の年齢の和
これを理解することが大切です。実際、計算する際は、
差が変わらない”親と子の年齢差”を基準に考えていきます。
早速みていきます。例題は、上記と同じものを使っていきます。
< 現在、父は30歳、子は4歳です。何年後に父の年齢が子の3倍になりますか。>
この”何年後かの父の年齢が子の3倍”を線分図にします。
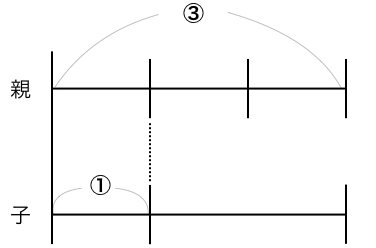
まず、何年進んでも変わらない親子の年齢差を計算します。
30 − 4 = 26
親と子の年齢差は、26歳です。これがいつ親が子の年齢の3倍になるかを考えます。
この26歳の年齢差は、図に示すとこのようになります。
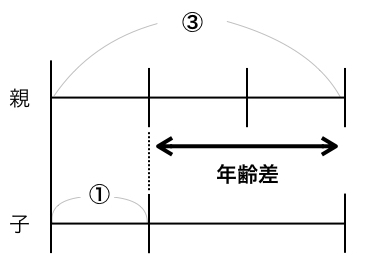
年齢差部分が26歳。各間隔は”等間隔”なので、”2間隔分=26″となります。
26 ÷ 2 = 13
1間隔 = 13なので、①は、13となります。つまり、子供が13歳の時、父の年齢が子の3倍になり、
現在、子は4歳なので、13 − 4 = 9
9年後と答えが出ます。方程式で解いた時と一緒です。
続いて、
< 現在、父と子の年齢の和は52歳。8年後に父の年齢は子の年齢の3倍になります。現在、父は何歳ですか。>
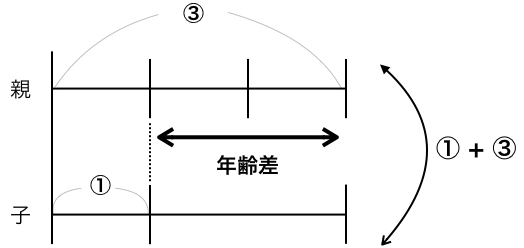
今度は、父と子の年齢の和(①+③)がわかっており、3倍になるのが8年後とあります。
現在の年齢の和が52なので、8年後は、父も子も8歳増えます(2人分)。
8年後は、52 + (8 x 2) = 68 父と子の和は、” 68 ” になります。
この時、3倍になるので、父と子の年齢比は 3 : 1。間隔が等間隔なので、4分の1は、子の年齢といえます。和が出ているので、
68 x 1/4 = 17
①が17歳(8年後の子の年齢)ですので、③は、51歳(8年後の父の年齢)です。
求められているのは、現在の父の年齢なので、
51 − 8 = 43
父は現在43歳です。こちらも方程式と同じ答えになりました。
簡単計算関連:確率 順列/組み合わせ 通過算/流水算 n進法
まとめ
方程式と線分図の基本を説明してきました。
どちらのやり方が正しいとかではなく、自身に合った方法または、問題による使い分けで、やりやすい方で良いです。
ここでは、基本的例を挙げました。連立方程式でも線分図でも
『求められている答えは何か。』
これに注意して解きます。どうしても、解いてる間に”これなんの計算だっけ?”となってしまいます。
一つ一つ、父母、子供が4人、何年前、何年後、現在、人数が増えたり、年数が前後であっても
『考え方は変わりません。』
・方程式なら ” x ” と ” y “を何にするのか。
・線分図なら、それぞれ間隔などが何を示しているのか。
こんなことをブレずに計算すれば、必然的に答えを導き出せます。
スポンサーリンク
