n進法の解き方と計算。n進法とはの基本から変換まで簡単理解。
投稿日：2018年7月3日 更新日：
n進法とは何なのと思う方もいるのではないでしょうか。例えば、普段使っているお金、1円が10枚になると10円玉、10円を10枚で100円。と10枚貯まると次の”位”の1枚と変わっていきます。”位”の繰り上げですが、このお金の繰り上げ例は、10進法と呼ばれる方法です。そして、1,2,3と数えていって初めて二桁になるのが”10″。一つの桁の中で利用できる数字は、０〜1の9個です。n進法のn部分が、2であれ、3であっても同じように考えていくのです。計算方法を含め、基本を押さえていきましょう。
n進法の基本概要
先の”お金”の例は、10進法といいましたが、これは、
｢一の位、十の位、百の位、千の位、万の位｣と位が上がるごとに数が10倍になっています。
つまり、
1 x 10 = 10
10 x 10 = 100
100 x 10 = 1,000
1,000 x 10 = 10,000
となるわけです。
2進法では2倍や３進法では3倍としていき、“次の位”として考えて計算していけば良いのです。
1 x 2 = 2 (2の位) 1 x 3 = 3 (3の位)
2 x 2 = 4 (4の位) 3 x 3 = 9 (9の位)
4 x 2 = 8 (8の位) 9 x 3 = 27 (27の位)
8 x 2 = 16 (16の位) 27 x 3 = 81 (81の位)
“位”の呼び方は違えど、考え方は同じなのです。これは、4進法でも5進法でも４倍する５倍するとしていくだけです。お金の理論に戻って考えれば、2枚集まったら次の位へという考えるのです。
このような考え方の詳細をみてみましょう。
例えば、”1,234″という数字がある場合、
一の位：４
十の位：３
百の位：２
千の位：1
です。この普段使っている”せんにひゃくさんじゅうよん”を計算式として分解していきます。
10倍になると次の位になるので、
と紐解くことができ、”せんにひゃくさんじゅうよん”は、計算式でこういう意味なのです。説明は不要かもしれませんが、10の上にある小さな数字は、”何乗”かを示していて、” 10 ” に “小さな３” で、10の３乗、10 x 10 x 10 =1,000 を示しています。
ここでは、４桁でしたが、さらに“位”が多くなれば、” 〜乗 “の部分は増えます。
例えば、4乗や5乗になります。
つまり、10進法に限らず、
” n個集まると1つ上の位に上がるn進法”であれば、
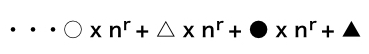※ ” r “は、桁数により変わる” r乗 “
という計算式になります。
n進法の計算
n進法の計算では、10進法をn進法へ、n進法を10進法へなど、この変換方法を知っておかなくてはいけません。
< 10進法をn進法へ >
例えば、10進法の33を2進法に変換するとき、33を割っていき、同じ行の欄外に“余り”を書いていきます。割り切れる場合には、欄外に余り” 0 (ゼロ) “です。
そして、” n “で割れる数字がなくなるまで、割り算をしていきます。
上記を計算すると、
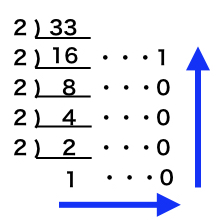
となります。最後 ” 1 “となっており、これ以上割ると分数になります。
そして、矢印の最初を起点に数字を並べていき、ここでは、
１０進法の33を2進法にすると、｢100001｣が答えです。
< n進法を10進法へ >
今度は、n進法を10進法へ変換します。やり方は何個かありますが、計算という意味で簡単な方法をここでは取り上げます。
先例の2進法｢110001｣を10進法にしてみましょう。
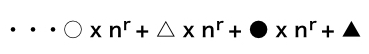
この公式に倣えば、
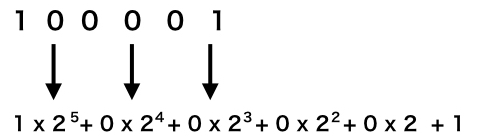
これを計算すると” 33 “となります。合ってますよね。一般的なやり方です。これをさらに簡単に計算していきます。
この” 100001″の間にn進法の”n”を掛ける( x n )として入れていきます。
すると、
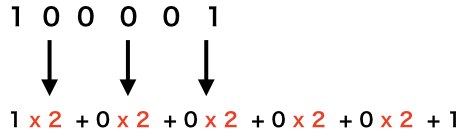
となります。これを四則演算(+−x÷の計算順序)を無視して、前から順番に計算します。
実際やってみます。
1 x 2 + 0 x 2 + 0 x 2 + 0 x 2 + 0 x 2 + 1
= 2 x 2 + 0 x 2 + 0 x 2 + 0 x 2 + 1
= 4 x 2 + 0 x 2 + 0 x 2 + 1
= 8 x 2 + 0 x 2 + 1
= 16 x 2 + 1
= 33
です。ここでは、四則演算のルールに則れば、0 x 2 = 0ですが、前から順になので、0にはなりません。0の部分は”+ 0 “の計算になることに注意が必要です。
簡単計算関連：確率 順列/組み合わせ 通過算/流水算 仕事量
まとめ
いかがでしたかn進法。n進法からの変換は、最後の計算が一番簡単ですよね。
基本的概要、意味とともに、計算を覚えれば、基本的なことは理解できます。
難しい計算もないので、覚えてモノにしましょう。
スポンサーリンク
